• Homogeneous 좌표계
• 변환 행렬
  • 행렬에 대한 소개
  • 평행이동 행렬
  • 단위행렬
  • 스캐일링 매트릭스
  • 회전 매트릭스
  • 누적 변환
• 모델, 뷰, 프로젝션 행렬
  • 모델 매트릭스
  • 뷰 매트릭스
  • 프로젝션 매트릭스
  • 변환 쌓기 : 모델뷰 매트릭스
• 다같이 놓기
• 연습문제

엔진이 배를 움직이는 것이 아니다. 배는 그 자리에 가만이 있으나 엔진이 이 세상을 회전해 움직이는 것이다.

Futurama

이부분은 모든 것에 있어 가장 중요한 단 하나의 튜토리얼입니다. 그러니 최소한 여덟번은 읽도록 하세요.

Homogeneous 좌표계

지금까지, 우리는 3D 버텍스를 (x,y,z) 트리플렛(세묶음;triplet)으로서 다루었습니다. 여기에 w 를 소개합니다. 우리는 이제 (x,y,z,w) 벡터를 사용합니다.

이게 무엇인지 곧 알게 될겁니다. 하지만 지금은, 이것만 기억해 두세요 :

• w == 1 이면, 벡터 (x,y,z,1) 은 공간에서의 위치 입니다.
• w == 0 이면, 벡터 (x,y,z,0) 은 방향입니다.

(사실, 이 부분은 머릿속에 영원이 박아둬야 합니다.)

이게 무슨 차이를 만든다는 거죠? 음, 회전에 대해서 보면, 이것은 아무것도 바뀌지 않아요. 당신이 점이나 방향을 회전 시키면, 같은 결과를 얻게 되죠. 하지만, 평행이동(translation;트랜스레이션) 에 관해서는 (당신이 점을 특정 방향으로 이동시킬때), 변화가 일어납니다. “어떤 방향으로 평행이동(Translate)시킨다” 이게 무슨 뜻일까요 ? 별건 없습니다.

Homogeneous 좌표계에서는 하나의 수학 공식을 사용해서 이어질 두 경우를 다루게 해줍니다.

변환 행렬

행렬에 대한 소개

간단히 말해, 행렬(matrix)이란 미리 정의해둔 개수의 행(rows)들 과 열(colums)들을 이용해서 여러개의 배열(array)을 합쳐놓은 것 입니다. 예를 들어, 2x3 행렬은 아래 처럼 보이겠죠 :

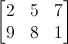
3D 그래픽스에서 4x4 행렬을 주로 사용합니다. 이들은 우리의 (x,y,z,w) 버텍스들을 변형하게 해줍니다. 이는 버텍스를 행렬로 곱하여 이루어집니다 :

행렬 x 버텍스 (이 순서로 곱해야 합니다!!) = 변형된_버텍스

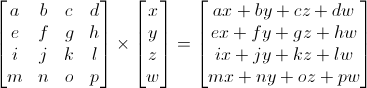
보는 것 만큼 무섭게 어렵진 않습니다. 왼쪽 손가락을 a 에 두고, 오른쪽 손가락을 x 에 둬 보세요. 이것이 ax 입니다. 왼쪽 손가락을 다음 숫자 (b) 에 두세요. 그리고 오른쪽 손가락을 다음 숫자 (y) 에 두세요. 당신은 by 를 얻었습니다. 다시 한번 : cz. 다시 한번 : dw. ax + by + cz + dw. 당신은 새로운 x 를 얻었네요 ! 각각의 줄에 똑같이 해보면, 당신은 새로운 (x,y,z,w) 벡터를 얻게 됩니다.

이 부분은 계산하기 지루한 부분입니다만, 자주 하게 될거에요. 그러니 앞으로는 컴퓨터에게 대신 해달라고 부탁하죠.

C++에서, GLM으로:

glm::mat4 myMatrix;
glm::vec4 myVector;
// myMatix 와 myVector 를 어떻게 채웁니다.
glm::vec4 transformedVector = myMatrix * myVector; // 다시한번 말하지만 이 순서로 곱하십쇼! 정말 중요합니다!

In GLSL :

mat4 myMatrix;
vec4 myVector;
// myMatrix 와 myVector 를 어떠한 방식으로 채웁니다
vec4 transformedVector = myMatrix * myVector; // Yeah, it's pretty much the same than GLM

( 이 부분을 당신의 코드에 잘라 붙여보았나요? 지금 한번 해보세요)

평행이동 행렬

이들은 가장 이해하기 쉬운 형태의 변형(tranformation) 입니다. 평행이동 행렬은 이렇게 생겼습니다 :

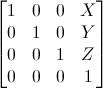
X,Y,Z 에 있는 것들이 당신의 위치에서 더하고자 하는 값들입니다.

그래서 벡터 (10,10,10,1) 을 X 방향으로 10 유닛(unit;이동단위, 현실의 어떤 길이에 매칭할 것인지는 개발자 마음.)만큼 평행시키려면 이런 식을 계산합니다 :

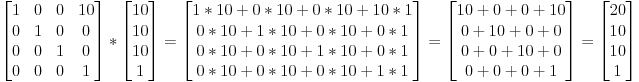
(그냥 하셈 ! 일다아아안 그냥 해보셈!!)

… 그리고 이제 (20,20,10,1) 호모지니어스 벡터를 얻었습니다 ! 기억하세요, 마지막 1은 우리가 위치가 아닌 방향을 다룬다는 의미입니다. 그러니 우리가 만든 변형이, 위치에 관해 다루고 있었단 사실은 바꾸지 않았단 얘기입니다. 좋은 일이죠.

이제 -z 축을 표현하는 벡터에게 어떤 일이 일어나는지 봅시다: (0,0,-1,0)

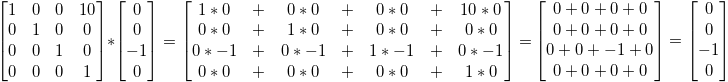
… 즉 이것이 오리지날 (0,0,-1,0) 방향입니다. 굉장한 일이죠, 제가 앞서 말했던 것 처럼, 방향을 움직인다는 것은 말이 안되죠.

그래서, 평행이동을 어떻게 코드로 수행 하나요?

C++ 에서, GLM을 사용:

#include <glm/gtx/transform.hpp> // after <glm/glm.hpp>

glm::mat4 myMatrix = glm::translate(glm::mat4(), glm::vec3(10.0f, 0.0f, 0.0f));
glm::vec4 myVector(10.0f, 10.0f, 10.0f, 0.0f);
glm::vec4 transformedVector = myMatrix * myVector; // guess the result

GLSL 에서 :

vec4 transformedVector = myMatrix * myVector;

음, 사실은, GLSL 에서는 이럴 일이 거의 없을거에요. 대부분의 시간 동안, 당신은 glm::translate() 를 C++ 에서 행렬을 계산하기 위해 쓸거고, 그걸 GLSL 에 보낼겁니다. 그리고 곱셈만 하겠죠 :

단위행렬

이것은 특별합니다. 이것은 아무것도 하지않아요. 하지만 말해둡니다. 왜냐하면 A에 1.0을 곱하면 A 가 된다는 사실을 아는 것은 중요하니까요.

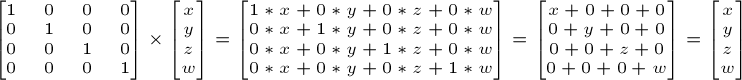
C++ 에서:

glm::mat4 myIdentityMatrix = glm::mat4(1.0f);

스캐일링 매트릭스

스케일링 매트릭스는 꽤나 쉽습니다 :

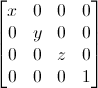
그래서 만약 벡터를 (위치나 방향은 상관없습니다) 모든 방향으로 2.0 배 스케일 하고 싶다면 :

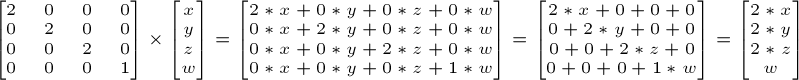
물론 w 는 아직 아무것도 바꾸지 않습니다. 질문이 생길지도 모르죠: “방향을 스케일링” 한다는 의미가 뭐죠 ? 음, 별건 없어요, 그럴일 은 별로 없을테니까요. 하지만 매우 드물게 유용한 경우도 있습니다.

(단위 매트릭스는 (X,Y,Z) = (1,1,1) 로서 스케일링 매트릭스의 유일한 경우임을 알아두세요. 또한 트랜스레이션 매트릭스의 (X,Y,Z) = (0,0,0) 으로서 특별한 경우이기도 합니다)

C++ 에서 :

// Use #include <glm/gtc/matrix_transform.hpp> and #include <glm/gtx/transform.hpp>
glm::mat4 myScalingMatrix = glm::scale(2.0f, 2.0f ,2.0f);

회전 매트릭스

이 부분은 조금 복잡할 수 있어요. 여기서는 자세한 사항은 생략합니다. 매일 사용하는데 있어 구체적인 레이아웃을 아는 것은 별로 중요하지 않아요. Matrices and Quaternions FAQ (popular resource, probably available in your language as well). You can also have a look at the Rotations tutorials 을 한번 봐주세요.

C++ 에서 :

// Use #include <glm/gtc/matrix_transform.hpp> and #include <glm/gtx/transform.hpp>
glm::vec3 myRotationAxis( ??, ??, ??);
glm::rotate( angle_in_degrees, myRotationAxis );

누적 변환

이제 우리는 벡터들을 어떻게 회전하고, 평행이동하고, 스케일 하는지 알게 되었습니다. 이들 변환들을 합칠수 있다면 굉장하겠죠. 이는 매트릭스들을 함께 곱함으로서 이루어집니다. 예를 들어 :

TransformedVector = TranslationMatrix * RotationMatrix * ScaleMatrix * OriginalVector;

!!! 주의사항 !!! 이 라인은 실제로는 스케일링을 먼저 하고나서 그 다음에 회전하고, 그 다음에 평행이동 합니다. 이것이 매트릭스 곱이 동작하는 법이에요.

연산을 다른 순서로 작성하는 것은 같은 결과를 내주지 않을 겁니다. 스스로 해보세요 :

• 한 걸음 간 다음에 (아, 컴퓨터 조심하세요.) 왼쪽으로 돌아보세요.

• 왼쪽으로 돈 다음에, 한 걸음 가보세요.

실제로, 위 순서는 게임 캐릭터나 다른 것들에게 꼭 필요한 것들이에요. : 확대가 필요하다면, 먼저 한 다음. 방향을 전하고, 이동하는 거에요. 예를 들어 볼까요? 배를 하나 가져다 놓을게요.

As a matter of fact, the order above is what you will usually need for game characters and other items : Scale it first if needed; then set its direction, then translate it. For instance, given a ship model (rotations have been removed for simplification) :

• 틀린 방법 :
  • 배를 (10, 0, 0) 으로 이동했어요. 이제 원점으로 부터 10 unit 떨어져 있네요.
  • 그리고 배를 2배로 키웠어요. 모든 좌표는 원점으로부터 상대적으로 2배 더 커졌고요. 어유. 멀리도 갔네. 확대가 끝나면 큰 배는 가지겠지만. 이제 원점으로 부터 2*10 = 20이나 멀어졌네요. 원하지 않는 선물을 받아버렸어요.
• 올바른 방법 :
  • 배를 2배 키워요. 그러면 큰 배를 얻었고, 원점에 잘 있죠.
  • 그리고 배를 이동시켜요. 여전히 같은 크기를 가지고 있고, 올바른 방향을 가지고 있죠.

행렬 - 행렬 곱은 행렬 - 벡터 곱가 아주 유사해요, 그래서 구체적인 내용을 생략하고. 대신 참고가 될 만한 링크를(Matricesa and Quaternions FAQ)걸어드릴게요. 만약에 행렬곱이 필요하다면. 지금은 그냥 컴퓨터에게 맡깁시다. :

Matrix-matrix multiplication is very similar to matrix-vector multiplication, so I’ll once again skip some details and redirect you the the Matrices and Quaternions FAQ if needed. For now, we’ll simply ask the computer to do it :

GLM과 함깨, C++에선. :

glm::mat4 myModelMatrix = myTranslationMatrix * myRotationMatrix * myScaleMatrix;
glm::vec4 myTransformedVector = myModelMatrix * myOriginalVector;

GLSL에선. :

mat4 transform = mat2 * mat1;
vec4 out_vec = transform * in_vec;

모델, 뷰, 프로젝션 행렬

튜토리얼의 남은 부분들에서는, 우리가 블랜더의 가장 사랑받는 3d 모델-키 수자네-을 그릴줄 이미 알고 있었다고 하고 진행합니다

모델과 뷰, 프로젝션 매트릭스는 변환들을 분명하게 구별하기 위한 좋은 도구 입니다. 이들을 안 쓸수도 있습니다 (여기까지 우리가 튜토리얼 1과 2에서 했던것 처럼). 하지만 써야만 합니다. 모든 사람이 이렇게 합니다. 왜냐면 이렇게 하는게 쉬운 길이니까요.

모델 매트릭스

이 모델, 우리의 사랑스런 붉은 삼각형 처럼, 여러가지 버텍스들로 정의 됩니다. 이들 버텍스들의 X,Y,Z 좌표들은 오브젝트의 중심에 상대적으로 정의됩니다 : 바로 그거에요. 만약 버텍스가 (0,0,0) 에 있다면, 오브젝트의 중심에 있는 겁니다.

이 모델을 움직이고 싶습니다. 플레이어가 이것을 키보드와 마우스로 조작할수도 있잖아요. 쉽게도, 당신은 방금 배웠어요 : ‘평행이동회전스케일’, 그리고 끝. 이 매트릭스를 매 프레임 마다 모든 버텍스들에 적용해야 합니다(GLSL 에서는, 움직이지 않은것은 월드의 중심 에 있습니다)

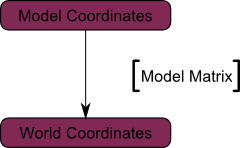
이제 당신의 버텍스들은 월드 공간_에 있습니다. 이것은 이미지의 검은 화살표를 의미합니다 : _모델 공간에서 (모든 버텍스들이 모델의 중심에 상대적으로 정의된 곳), 월드 공간 (모든 버텍스들이 월드의 중심에 상대적으로 정의된 곳) 으로 갔습니다.

우리는 이것을 이어지는 다이어그램으로 종합할수 있습니다 :

뷰 매트릭스

Futurama 의 말을 다시 이용해보죠 :

엔진이 배를 움직이는 것이 아니다. 배는 그 자리에 가만이 있으나 엔진이 이 세상을 회전해 움직이는 것이다.

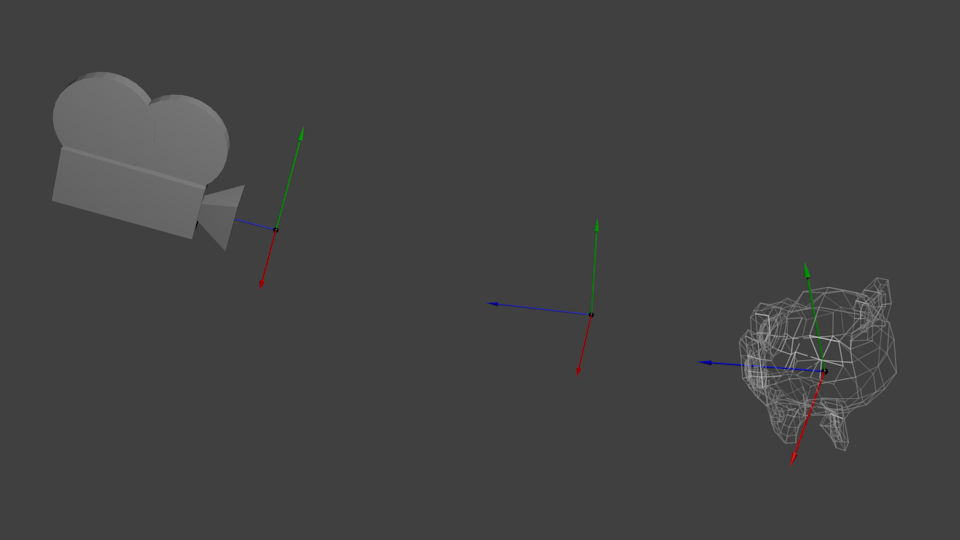
이것에 대해 생각해보면, 같은 의미가 카메라에도 적용됩니다. 만약 산을 다른 각도로 보고 싶다면, 당신은 카메라를 옮기거나… 아니면 산을 옮길수 있겠죠. 실제 세상에서는 불가능 하지만, 이곳은 모든 게 간단하고 유용한 컴퓨터 그래픽스 입니다.

그래서, 초기에는 당신의 카메라가 월드 좌표의 원점에 있습니다. 세상을 움직이기 위해서는, 간단히 새로운 매트릭스를 쓰면 됩니다. 당신이 카메라를 오른쪽 (+X) 으로 3 유닛 만큼 움직인다 하죠. 이것은 전체 세상을 (메쉬들을 포함해서) 3 유닛 왼쪽 (-X) 으로 움직이는 것과 같습니다 ! 당신 두뇌가 녹기전에, 어서 해보죠 :

// Use #include <glm/gtc/matrix_transform.hpp> and #include <glm/gtx/transform.hpp>
glm::mat4 ViewMatrix = glm::translate(glm::mat4(), glm::vec3(-3.0f, 0.0f, 0.0f));

또다시, 아래 이미지가 표현하는 바는 : 우리는 월드 공간 (모든 버텍스들이 월드의 중심에 상대적인 곳, 지난 섹션에서 다루었죠) 에서 카메라 공간 (모든 버텍스들이 카메라에 상대적으로 정의되는 곳) 으로 갔습니다.

당신의 두뇌가 터져버리기 전에, GLM의 훌륭한 glm::lookAt 함수를 즐겨봅시다:

glm::mat4 CameraMatrix = glm::lookAt(
    cameraPosition, // 월드 공간에서 당신의 카메라 좌표
    cameraTarget,   // 월드 스페이스에서 당신의 카메라가 볼 곳
    upVector        // glm::vec(0,1,0) 가 적절하나, (0,-1,0)으로 화면을 뒤집을 수 있습니다. 그래도 멋지겠죠
);

또 강제로 다이어그램을 끌고 왔습니다 :

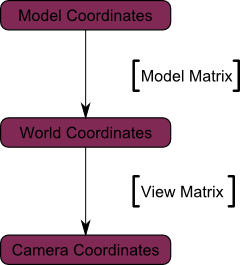
하지만 사실 아직 끝이 아니에요.

프로젝션 매트릭스

우리는 이제 카메라 공간에 왔어요. 이는 모든 이 모든 변환들이 끝난후, x==0 과 y==0 을 가지게 되는 버텍스는 스크린의 중앙에 그려질거란 거죠. 하지만, 오브젝트를 스크린 어디에 띄울지 결정할때 x 와 y 좌표만 사용하는건 불가능 해요: 카메라로 부터의 거리 (z) 도 물론 세야 합니다 ! x 와 y 좌표가 비슷한 두개의 버텍스들 끼리도, z 값이 큰 버텍스는 다른 것들보다 화면의 중심에 더 가까워 집니다.

이것을 perspective 프로젝션 이라 부릅니다 :

그리고 우리 모두에게 다행이도, 4x4 매트릭스는 프로젝션[^프로젝션] 을 표현할수 있습니다 :

// Generates a really hard-to-read matrix, but a normal, standard 4x4 matrix nonetheless
glm::mat4 projectionMatrix = glm::perspective(
    glm::radians(FoV),  // 수직방향 시야각입니다 : "줌"의 크기. "카메라 렌즈" 를 생각해보세요. 이들은 보통 90도 (엑스트라 와이드) 에서 30도 (크게 확대한 경우) 사이에 있습니다
    4.0f / 3.0f, // 화면 비 입니다. 이것은 당신의 윈도우 크기에 의존합니다. 4/3 == 800/600 == 1280/960 인데, 어디서 본것 같죠 ?
    0.1f,        // Near clipping plane (근거리 잘라내기 평면). 최대한 크게 하세요. 아니면 정확도 문제가 생길 수 있습니다.
    100.0f       // Far clipping plane (원거리 잘라내기 평면). 최대한 작게 하세요.
);

마지막으로 :

우리는 카메라 공간 (모든 버텍스들이 카메라 좌표에 상대적) 에서 호모니지어스 공간 (모든 버텍스들이 작은 큐브 안에 정의되고, 큐브안에 있는 모든 것들은 화면에 띄어집니다)으로 갔습니다.

그래서 마지막 다이어그램 :

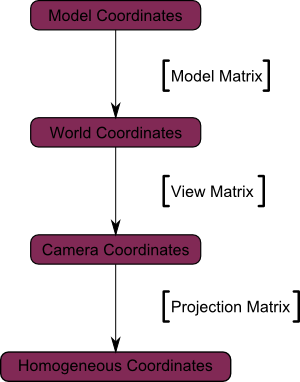
여기 또다른 다이어그램이 있어, 프로젝션이 어떤 일을 하는지 이해하기 쉬울 겁니다. 프로젝션 전에, 우리는 블루 오브젝트들이 카메라 공간에 있었어요. 그리고 레드 모양은 카메라의 프러스텀을 표현합니다 : 카메라가 실제로 보게되는, 씬의 일부요.

모든 것들을 프로젝션 매틀픽스로 곱하는 것은 아래와 같은 효과를 줍니다 :

이 이미지에서, 프러스텀은 이제 완벽한 큐브 (눈으로 잘 파악되지 않지만, 모든 축으로 -1에서 1사이만 존재합니다)가 되었습니다. 그리고 모든 블루 오브젝트들도 같은 방식으로 왜곡되었죠. 따라서, 카메라 근처의 오브젝트 ( = 이미지에서 우리가 못보는 쪽 큐브의 면 근처) 은 크게 되고, 다른 것들은 작아집니다. 실제 세상에서 처럼요 !

이제 프러스텀 “뒤”에서 어떻게 보이는지 봅시다 :

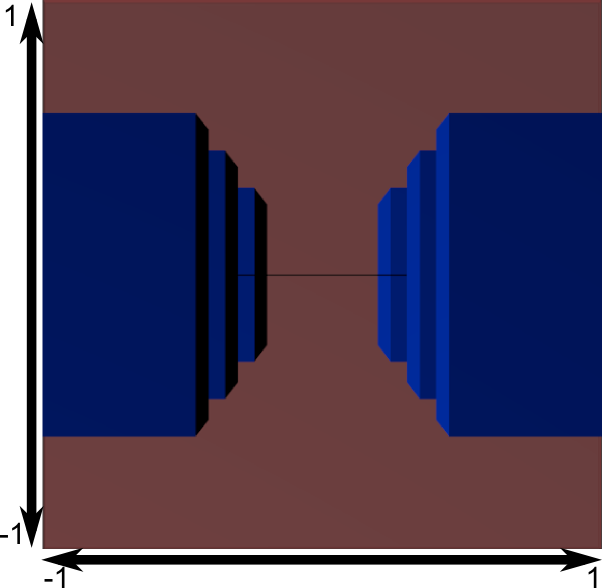
여기 당신의 이미지를 얻었네요 ! 너무 정사각형 인데, 또다른 수학적인 변환이 적용되어 (이것은 자동으로 됩니다. 셰이더로 직접 하지 않아도 되요) 실제 윈도우 사이즈에 맞추어집니다 :

그리고 여기 실제로 랜더 되는 이미지가 있네요 !

변환 쌓기 : 모델뷰 매트릭스

… 당신이 이미 사랑했었던 일반적인 매트릭스 곱과 같습니다 !

// C++ : 매트릭스 계산하기
glm::mat4 MVPmatrix = projection * view * model; // 기억하기 : 순서가 뒤집힘 !

// GLSL : 적용하기
transformed_vertex = MVP * in_vertex;

다같이 놓기

• 첫번째 : MVP 매트릭스를 생성합니다. 랜더하는 각각의 모델마다 반드시 해주어야 합니다.

  // 프로젝션 매트릭스 : 45도 시야각, 4:3 비율, 시야 범위 : 0.1 유닛 <--> 100 유닛
  glm::mat4 Projection = glm::perspective(glm::radians(45.0f), (float) width / (float)height, 0.1f, 100.0f);
  
  //혹은 ortho(직교) 카메라에선 :
  //glm::mat4 Projection = glm::ortho(-10.0f,10.0f,-10.0f,10.0f,0.0f,100.0f); // 월드 좌표로 표현
  
  // 카메라 매트릭스
  glm::mat4 View = glm::lookAt(
      glm::vec3(4,3,3), // 카메라는 (4,3,3) 에 있다. 월드 좌표에서
      glm::vec3(0,0,0), // 그리고 카메라가 원점을 본다
      glm::vec3(0,1,0)  // 머리가 위쪽이다 (0,-1,0 으로 해보면, 뒤집어 볼것이다)
      );
  
  // 모델 매트릭스 : 단위 매트릭스 (모델은 원점에 배치된다)
  glm::mat4 Model = glm::mat4(1.0f);
  // 우리의 모델뷰프로젝션 : 3개 매트릭스들을 곱한다
  glm::mat4 mvp = Projection * View * Model; // 기억하세요, 행렬곱은 계산은 반대순서로 이루어집니다
  

• 두번째 : GLSL에게 줘버려요.

  // 우리의 "MVP" 행렬에 참조를 얻습니다. 
  // 아. 초기화때만 하셔야 해요. 
  GLuint MatrixID = glGetUniformLocation(programID, "MVP");
  
  // 현재 바인딩된 쉐이더에게 변환한 메트릭스를 보냅시다. 방금 얻은 참조로요. 
  // 이건 각각의 모델마다 다른 MVP 행렬을 가지고 있을 것이니, 메인 루프에 해줍시다. (VP는 같을지 몰라도, M은 다를거에요.)
  glUniformMatrix4fv(MatrixID, 1, GL_FALSE, &mvp[0][0]);
  

• 세번쨰 : 우리가 GLSL에게 넘겨준 행렬을 정점에 적용시킵시다.

  //  vertex 데이터 입력 값, 쉐이더의 실행때마다 값이 다릅니다. 
  layout(location = 0) in vec3 vertexPosition_modelspace;
  
  //  이 값은 한 매쉬동안은 상수적입니다.  
  uniform mat4 MVP;
  
  void main(){
    // 정점의 출력 좌표, clip space에선 : MVP * position 
    // Output position of the vertex, in clip space : MVP * position
    gl_Position =  MVP * vec4(vertexPosition_modelspace,1);
  }
  

• 끝났어요! 튜토리얼 2와 같은 삼각형이 있을거에요. 아직도 원점 (0,0,0)에 있는 거 말이죠. 하지만 perspective로 (4,3,3) 좌표에서, 상향 벡터는 (0,1,0)으로 줬으니 45도 각도로 보일거에요.

튜토리얼 6에서는 키보드와 마우스를 이용해서 어떻게 우리가 오늘 썼던 값을 다이나믹하게 바꿀 수 있는지 배울거에요 - 마치 게임 카메라 같을걸요? - 하지만. 우선은 우리의 3D 모델에 어떻게 색상을 넣는지 (tutorial 4)와 텍스쳐를 넣을지부터 배울거에요. (tutorial 5)

연습문제

• glm::perspective를 한번 바꿔보세요.
• perspective(원근법) projection(투영법)을 쓰는 대신, orthographic projection을 써보세요. (glm::ortho)
• ModelMatrix를 이동하고, 회전하고, 확대해서 삼각형을 수정해보세요.ㅗ
• 같은 걸 해보시는데, 한번 다른 순서로 해보시겠어요? 어떤게 최고의 방법이었나요? 어떤 순서로 해야 캐릭터가 예쁘게 보일 것 같았나요?

Addendum