Picking with custom Ray-OBB function
This last method is a nice middleground between the “hacky” pure-OpenGL implementation, and having to integrate a fully-featured physics engine just to do raycasts and picking.
This tutorial uses concepts and functions from the Bullet tutorial, so make sure you read it first.
The basic idea
Instead of relying to Bullet intersect a ray with a Collision Shape, we’re going to do this ourselves.
As we have seen, there are many possible collision shapes. Spheres are very easy to intersect, but for many object, they represent the original mesh very poorly. On the other side, intersecting the ray with each triangle of the original mesh is way to costly. A good middleground are OBB : Oriented Bounding Boxes. There are quite precise (but it depends on your input geometry), and quite cheap to compute.
An OBB is a box that fits the mesh, and when the mesh is translated or rotated, the same transformation is applied to the box :
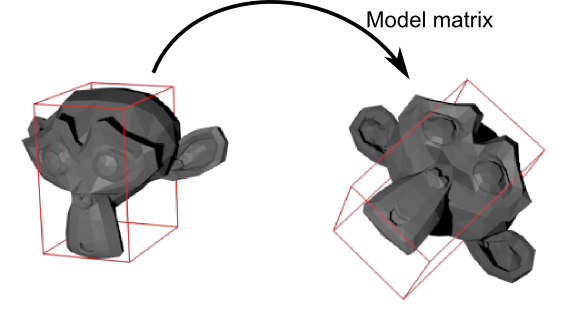
Ray-OBB intersection algorithm
( The algorithm and the pictures are largely inspired from Real-Time Rendering 3. Buy this book ! )
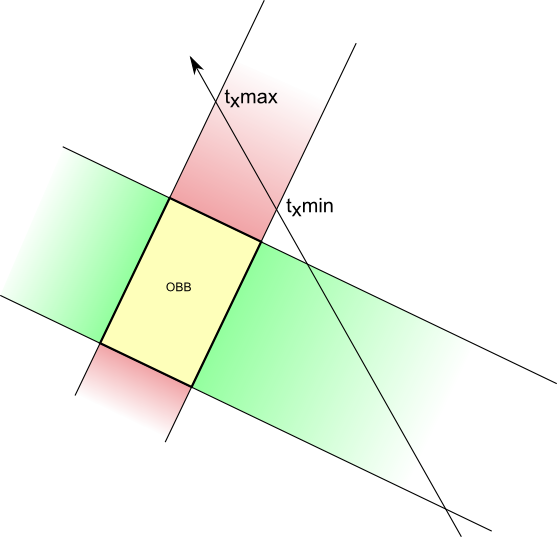
Consider the OBB below. On the X axis, this is delimited by 2 vertical planes, colored in red here. When intersected with the ray (a very simple operation), it gives 2 intersections, one “near” and one “far” :
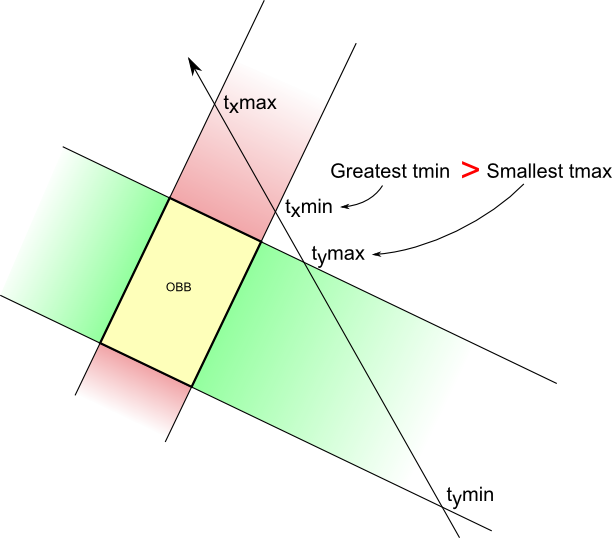
When the ray intersects the 2 others planes that delimit the Y axis (in green), it gives 2 more intersections. Notice how the intersections are ordered : you enter the green area -> you leave the green area -> you enter the red area -> you leave the red area. This means that there is no intersection.
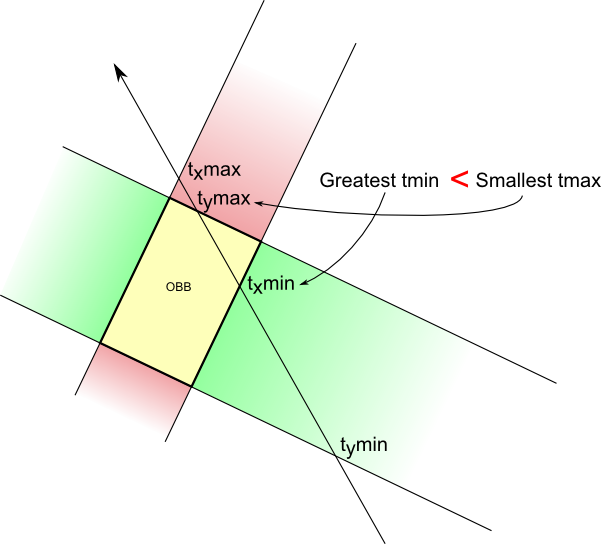
But if this order changes (you enter the green area -> you enter the red area), then you know there is an intersection !
Let’s put this in practice.
Algorithm implementation
(full source code is available in Misc05/misc05_picking_custom.cpp)
Our Ray - OBB intersection function will look like this :
bool TestRayOBBIntersection(
glm::vec3 ray_origin, // Ray origin, in world space
glm::vec3 ray_direction, // Ray direction (NOT target position!), in world space. Must be normalize()'d.
glm::vec3 aabb_min, // Minimum X,Y,Z coords of the mesh when not transformed at all.
glm::vec3 aabb_max, // Maximum X,Y,Z coords. Often aabb_min*-1 if your mesh is centered, but it's not always the case.
glm::mat4 ModelMatrix, // Transformation applied to the mesh (which will thus be also applied to its bounding box)
float& intersection_distance // Output : distance between ray_origin and the intersection with the OBB
){
We begin by nitializing a few variables. tMin is the largest “near” intersection currently found; tMax is the smallest “far” intersection currently found. Delta is used to compute the intersections with the planes.
float tMin = 0.0f;
float tMax = 100000.0f;
glm::vec3 OBBposition_worldspace(ModelMatrix[3].x, ModelMatrix[3].y, ModelMatrix[3].z);
glm::vec3 delta = OBBposition_worldspace - ray_origin;
Now, let’s compute the intersections with the 2 planes that delimit the OBB on the X axis :
glm::vec3 xaxis(ModelMatrix[0].x, ModelMatrix[0].y, ModelMatrix[0].z);
float e = glm::dot(xaxis, delta);
float f = glm::dot(ray_direction, xaxis);
// Beware, don't do the division if f is near 0 ! See full source code for details.
float t1 = (e+aabb_min.x)/f; // Intersection with the "left" plane
float t2 = (e+aabb_max.x)/f; // Intersection with the "right" plane
t1 and t2 now contain distances betwen ray origin and ray-plane intersections, but we don’t know in what order, so we make sure that t1 represents the “near” intersection and t2 the “far” :
if (t1>t2){ // if wrong order
float w=t1;t1=t2;t2=w; // swap t1 and t2
}
We can update tMin and tMax :
// tMax is the nearest "far" intersection (amongst the X,Y and Z planes pairs)
if ( t2 < tMax ) tMax = t2;
// tMin is the farthest "near" intersection (amongst the X,Y and Z planes pairs)
if ( t1 > tMin ) tMin = t1;
And here’s the trick : if “far” is closer than “near”, then there is NO intersection.
if (tMax < tMin )
return false;
This was for the X axis. On all other axes it’s exactly the same !
Using the algorithm
The TestRayOBBIntersection() functions enables us to test the intersection with only one OBB, so we have to test them all. In this tutorial, we simply test all boxes one after the other, but if you have many objects, you might need an additional acceleration structure like a Binary Space Partitionning Tree (BSP-Tree) or a Bounding Volume Hierarchy (BVH).
for(int i=0; i<100; i++){
float intersection_distance; // Output of TestRayOBBIntersection()
glm::vec3 aabb_min(-1.0f, -1.0f, -1.0f);
glm::vec3 aabb_max( 1.0f, 1.0f, 1.0f);
// The ModelMatrix transforms :
// - the mesh to its desired position and orientation
// - but also the AABB (defined with aabb_min and aabb_max) into an OBB
glm::mat4 RotationMatrix = glm::toMat4(orientations[i]);
glm::mat4 TranslationMatrix = translate(mat4(), positions[i]);
glm::mat4 ModelMatrix = TranslationMatrix * RotationMatrix;
if ( TestRayOBBIntersection(
ray_origin,
ray_direction,
aabb_min,
aabb_max,
ModelMatrix,
intersection_distance)
){
std::ostringstream oss;
oss << "mesh " << i;
message = oss.str();
break;
}
}
Note that this algorithm has a problem : it picks the first OBB it finds. But if this OBB is behind another OBB, this is wrong. So you would have to take only the nearest OBB ! Exercise left to the reader…
Pros and cons
Pros :
- Easy
- Low memory requirements (just the OBB’s extents)
- Doesn’t slows OpenGL down as the 1rst version
Cons :
- Slower than a physics engine since there is no acceleration structure
- Might not be precise enough.
Final remarks
There are many other intersection routines available for all sorts of collision shapes; see http://www.realtimerendering.com/intersections.html for instance.
If you need precise intersection, you will have to test ray-triangle intersections. Again, it’s not a good idea to check each triangle of each mesh linearly. Another acceleration structure is required.