Trigonometry

Pi

const float pi = 3.14159265f; // but an infinity of digits in reality

Cosinus & Sinus

(From http://commons.wikimedia.org/wiki/User:Geek3 , under GNU Free Documentation License )

Unit circle

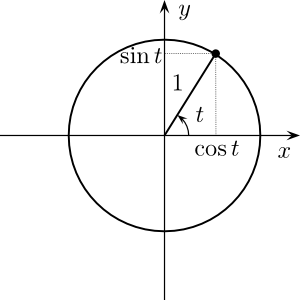
( Modified from http://en.wikipedia.org/wiki/User:Gustavb under Crative Commons 3.0 )

t is an angle in radians.

0 radians = 0 degrees

180 degrees = Pi radians

360 degrees ( full circle ) = 2*Pi radians

90 degrees = Pi/2 radians

Vectors

ALWAYS know in which coordinates your vector is. See section 3 for details.

Homogeneous coordinates

A 3D vector is (x,y,z), but a homogeneous 3D vector is (x,y,z,w).

• w=0 : it’s a direction
• w=1 : it’s a position
• else : it may still be correct, but you’d better know what you’re doing.

You can only multiply a 4×4 matrix with a homogeneous vector.

Length

Just like cartesian distance : sqrt( x² + y² + z² ). w doesn’t count.

Cross product

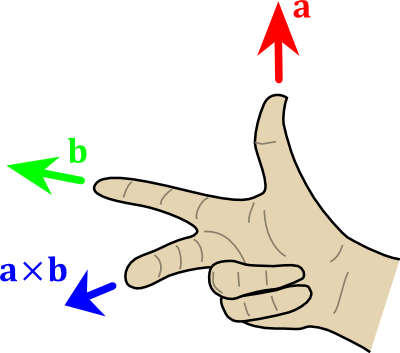
( Modified from http://en.wikipedia.org/wiki/User:Acdx , former image under Creative Commons 3.0 )

The X is the notation for the cross product. length( a x b ) == length(a) * length(b), so you may want to normalize() the result.

Dot product

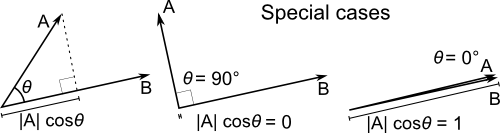
( from http://en.wikipedia.org/wiki/File:Dot_Product.svg )

A.B = length(A)*cos(Theta) , but most likely computed as A.x*B.x +A.y*B.y +A.z*B.z

Addition and substraction

compontent-wise :

res.x = A.x + B.x
res.y = A.y + B.y
...

 

Multiplication

compontent-wise :

res.x = A.x * B.x
res.y = A.y * B.y
...

Normalization

Divide the vector by its length :

normalizedVector = vec * ( 1.0f / vec.length() )

Matrices

Matrix-Matrix multiplication

example for a translation matrix :

 

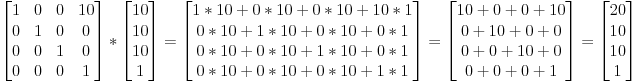
Matrix-Vector multiplication

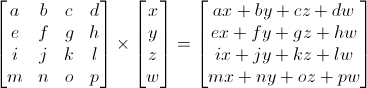
Usual Transformations

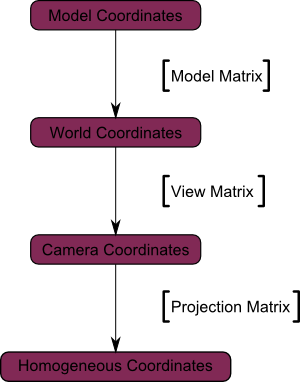
… but in your shaders, you can also represent your vectors in tangent space. And in image-space when you do post-effects.